Kinematic Analysis of Mechanism
What do we mean by kinematic analysis of a mechanism ?
Analyzing the motion of a mechanism without consideration of the forces causing them .
The goals of a kinematic analysis?
- Understand how each part moves relative to others.
- Calculate displacements, velocities, and accelerations of all points and links.
- Ensure the mechanism will perform the desired motion correctly.
- Position Analysis:
- Determines the location of all parts of the mechanism at a specific instant.
- Uses geometry or trigonometry.
- Calculates the speed and direction of movement for different parts.
- Often uses relative velocity equations, instantaneous center of rotation, or vector analysis.
- Determines how velocity changes over time.
- Important for understanding the dynamic behavior of the mechanism.
Why is doing kinematic analysis important ?
it allows engineers and designers to understand and predict how a mechanical system will move.
- Ensures Proper Functionality
- Design Optimization
- Dynamic and Force Analysis
- Improves Safety and Reliability
- Avoiding excessive wear or stress.
- Reducing vibration and noise.
- Ensuring smooth operation
Kinematic analysis of a 4 bar mechanism :
Here is a line diagram of a 4 bar link mechanism:
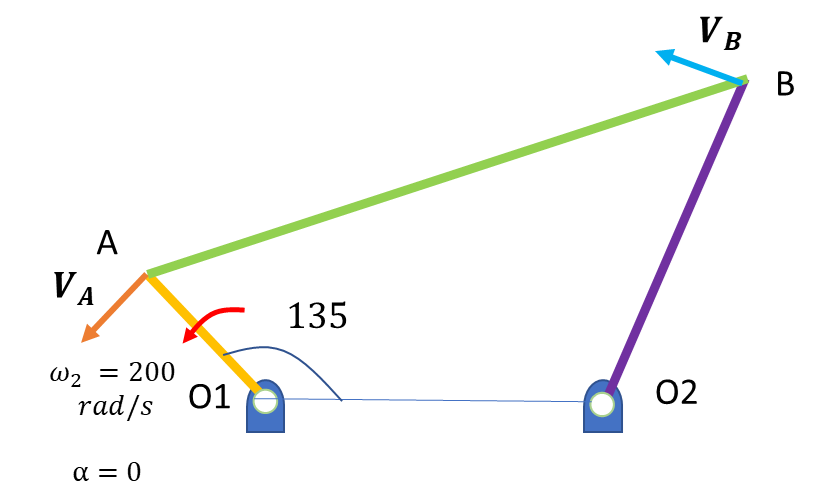
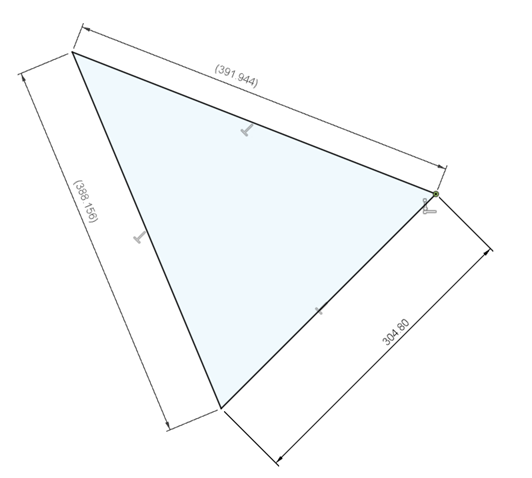
A-O1 is the crank which rotates at 200 rad/s .
Due to rotation of the crank the points A and B will undergo change in position and accelerate.
The Linear Velocities at point A and at point B will be in the direction as shown
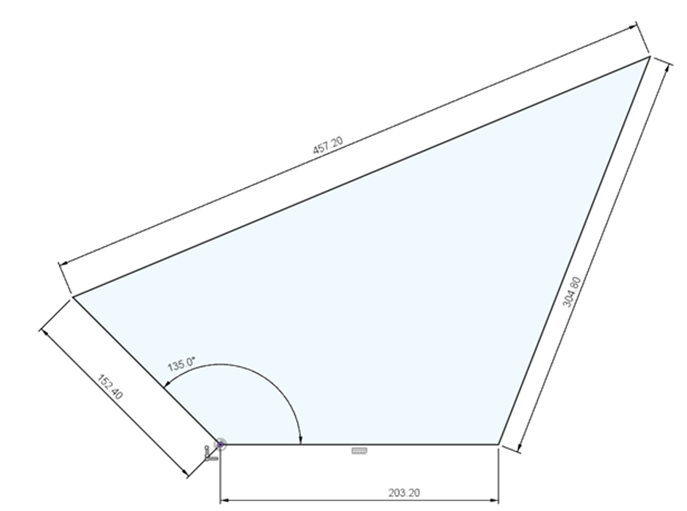
Position analysis and Dimensions of the links in using CAD:
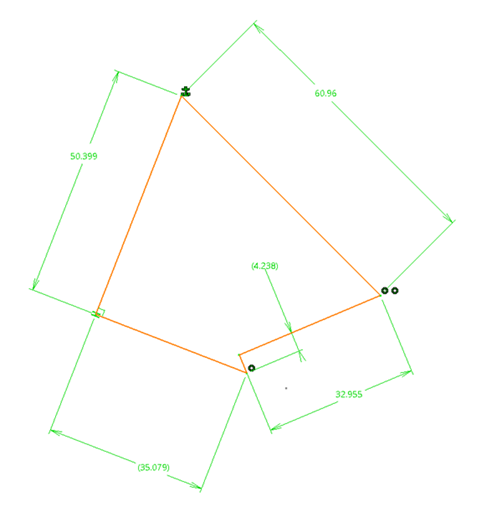
Velocity polygon for the mechanism:
The velocity of the points A and B are known in direction , Velocity at point A can be found using angular velocity and radius of arm . Hence the relative velocity of point B with respect to A can be found .
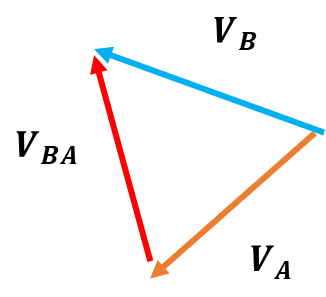
Using the input angular velocity all other linear velocities can be found .
Graphical solution of the velocity polygon:
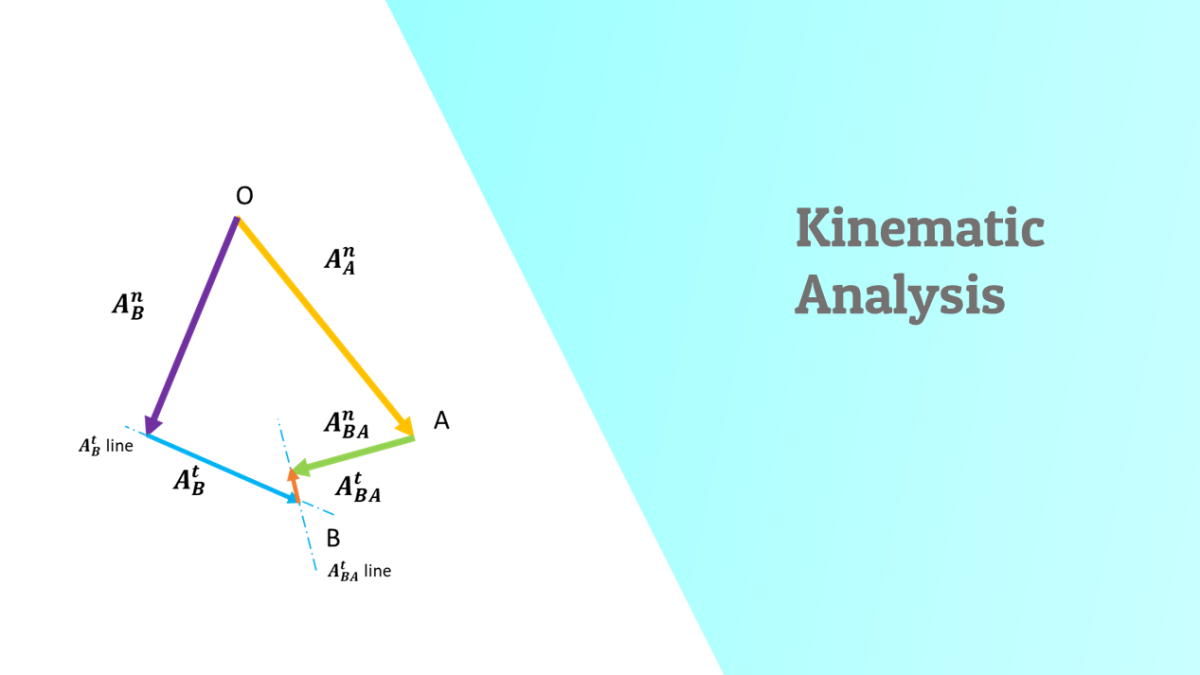
Acceleration Analysis of the 4 bar mechanism :
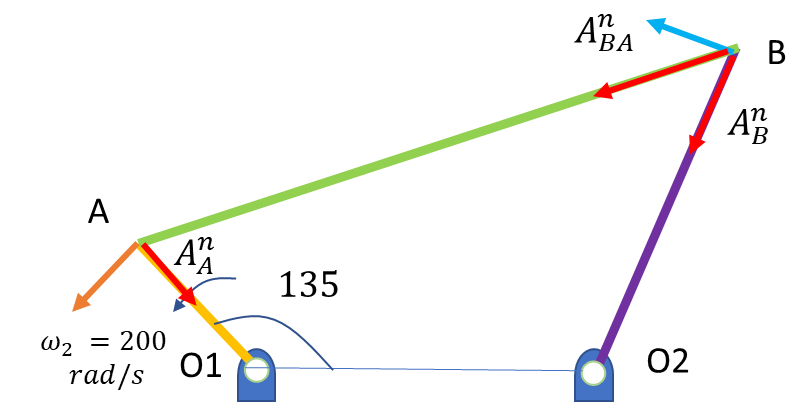
The acceleration at point A and B has a transverse component and normal component with respect to their rotation centres .
Using the graphical method, the acceleration polygon can also be plotted as :
Direction of transverse acceleration at A and normal acceleration at A are known , similarly the directions of transverse and normal components of accelerations at point B are also known .
Using relations between linear velocity and accelerations , the magnitudes can be found .
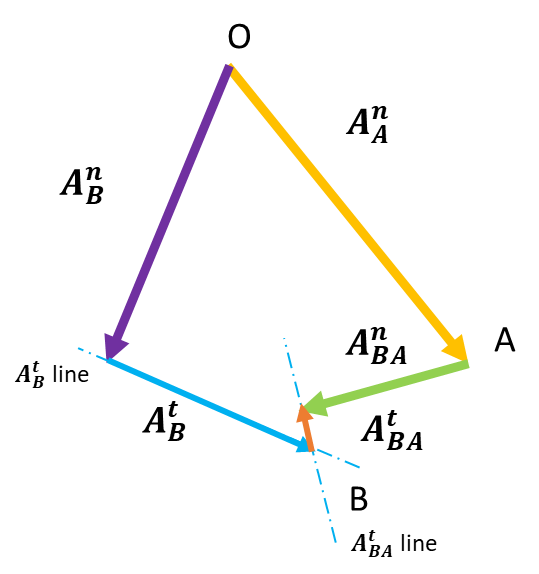
The graphical solution for each acceleration components can be found
Categories: : Mechanism and Machine design
 Mufaddal Rasheed
Mufaddal Rasheed 